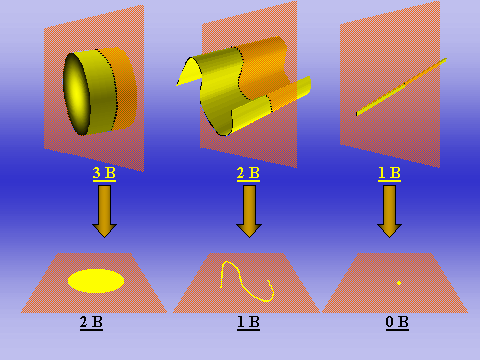

Şekil 1: İki boyutlu kesitlerle yapılan örneklemelerde ortaya çıkan boyut azalması. Herhangi bir yapı, iki boyutlu bir düzlemle kesişmesi durumunda, normalde üç boyutlu uzaydaki n boyutlu yapısına bağlı olarak, n-1 boyutlu bir kesişim (izdüşüm) verir. Dolayısıyla iki boyutlu kesitlerde, hacme sahip 3 boyutlu yapılar iki boyutlu alanlar; iki boyuta (en ve boy) sahip alanlar tek boyutlu çizgiler; ve tek boyutlu çizgiler ise boyutsuz (sıfır boyutlu) noktalar olarak örneklenirler. Bu durum biyolojik dokulara uyarlanacak olursa: Bir hücre (3 boyutlu), kesitte bir alan; bir zar bir çizgi (çekirdek zarı gibi) ve (tam olmasa da ideal anlamında bir çizgi olan) bir fibril de bir nokta olarak ortaya çıkacaktır. Bu prensibe göre boyutsuz (sıfır boyutlu) varlıklar, iki boyutlu kesitlerle örneklenemezler. Sayı kavramı da, boyutsal özelliklerden bağımsız (yani sıfır boyutlu) olduğundan, iki boyutlu kesitlerden faydalanılarak, doğrudan sayı kavramına ulaşmak imkansızdır. Sayı ancak üç boyutlu bir örnekleme sondası ile örneklenebilir.